El control de las carteras de renta fija es fundamental a la hora de buscar la mayor rentabilidad minimizando el riesgo. Todo activo de renta fija está sujeto a variaciones de precio y con ello hay un riesgo de pérdida de valor del mismo. Por ello, es importante controlar este riesgo y las posibilidades de depreciación (también de revalorización) de nuestro valor de renta fija o cartera (si combinamos varios de estos activos).
En primer lugar, lo hacemos con la duración, que no deja de ser una medida del plazo de maduración del bono. Se analizan los reembolsos (pagos de cupones), que va a recibir el bono y se ponderan dentro del precio del valor de renta fija. Con ello, se mide el riesgo de la exposición del bono o cartera a las variaciones de tipos interés. Cuanto mayor sea la duración, mayor es la subida del precio del bono cuando los tipos de interés bajan, y mayor es el descenso de dicho precio en la situación contraria.
La importancia de la convexidad
Pero la duración no es el único concepto que tenemos que tener en cuenta a la hora de medir los riesgos de un bono y elegir las mejores opciones. Otra medida, la convexidad, es fundamental.
Este concepto se denomina así porque la curva decreciente que liga el precio del bono y su rentabilidad (Tasa Interna de Rendimiento, TIR) es matemáticamente convexa, o lo que es lo mismo, la línea tangente en cualquier punto queda por debajo de la curva. Es decir, subestima el valor de la función en cualquier otro punto del entorno.
¿Qué aplicaciones prácticas tiene? Con la convexidad medimos la variación en la duración del bono para un cambio en la rentabilidad y con ello permite mejorar la aproximación de la duración para variaciones en los precios de los bonos.
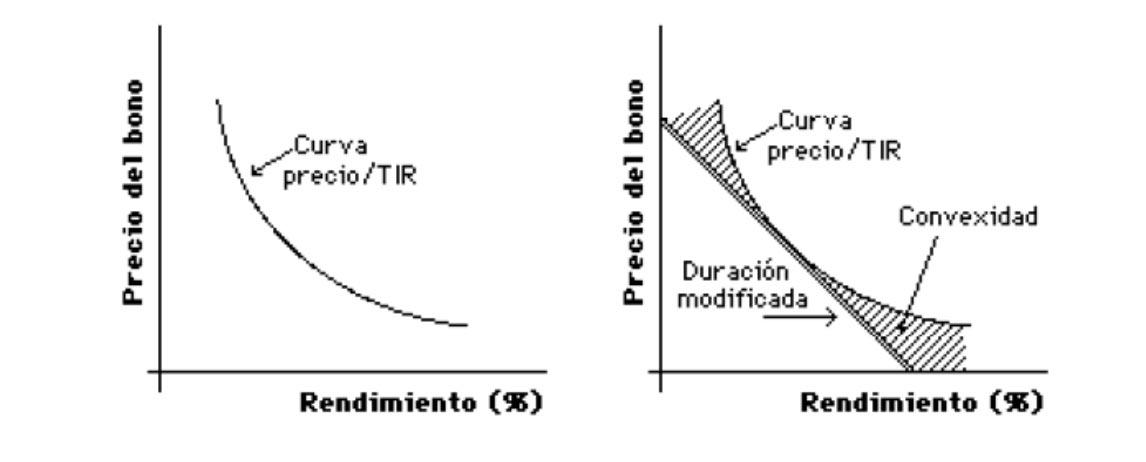
Aunque la teoría suene compleja, la aplicación práctica es clara. A igualdad de precios se preferirá siempre el bono más convexo, ya que permite que si los tipos de interés disminuyen se incremente más el valor y análogamente, si los tipos de interés aumentan disminuye menos.
Un ejemplo de su aplicación práctica
Supongamos un bono emitido a 20 años con un cupón del 9% a un precio de 134,6 € y una TIR del mercado del 6%, es decir que si compramos un bono similar en el mercado secundario nos pagarían un 3% menos que lo que nos rinde el que tenemos en propiedad, que nos paga un cupón del 9%.
Calculamos las variables principales:
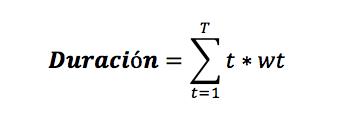
Duración = {6/(1,09) + 2*6/(1,09)^2 + 3*6/(1,09)^3 + 4*6/(1,09)^4 + 5*6/(1,09)^5+6*6/(1,09)^6+7*6/(1,09)^7+8*6/(1,09)^8+9*6/(1,09)^9+10*6/(1,09)^10+11*6/(1,09)^11+12*6/(1,09)^12+13*6/(1,09)^13+14*6/(1,09)^14+15*6/(1,09)^15}/134,672 = 10,98
Duración Modificada: Duración / 1 + diferencia tipos de interés y TIR = 10,98 / (1 + (0,09-0,06)) = 10,98 / 1,03 = 10,66
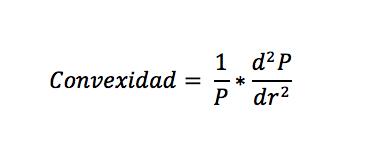
Convexidad = (1/134,672)*((10,98^2*134,672)/(0,03) )^2) = 164,106
Si por ejemplo el tipo de interés sube del 6% al 8%, sucedería lo siguiente:
La duración desciende: -10,66 x 0,02 x 100 = -21,32%
La convexidad aumenta: 0,5 x 164,106 x (0,02)^2 x 100 = +3,28%
Y la total variación del precio esperado desciende globalmente: -21,32% + 3,28% = -18,04%
Todo ello es debido a que, aunque nuestro bono sigue siendo atractivo con respecto al mercado, lo es menos globalmente.
Por el contrario, si los intereses de mercado varían en sentido contrario, del 6% al 4%, se produciría este efecto:
Nuestra duración sube: -10,66 x -0,02 x 100 = 21,32
La Convexidad lo haría en el mismo sentido, ya que la variación es del 2% (aunque en este caso negativa): 0,5 x 164,106 x (-0,02)^2 x 100 = +3,28%
Total variación en precio esperada = 21,32% + 3,28% = 24,60%
Es decir, si bajan los tipos de interés de mercado, nuestro bono o cartera es más rentable.
La importancia de la convexidad
Con este ejemplo vemos como la convexidad mejora y ayuda analizar la cartera de renta fija. A igualdad de rentabilidad y duración, se prefieren las carteras más convexas a las menos convexas. De hecho muchas carteras combinan activos, unos con la menor duración posible junto con otros de elevada duración, a fin de obtener convexidades elevadas, que permitan clasificar a estas carteras como muy sensibles a los descensos del tipo de interés y a la vez no tan sensibles al aumento de los tipos.
Por todo ello, esta herramienta aparentemente compleja es fundamental para que los gestores consigan el máximo rendimiento de carteras y fondos de inversión de renta fija y especialmente, para controlar el riesgo.





